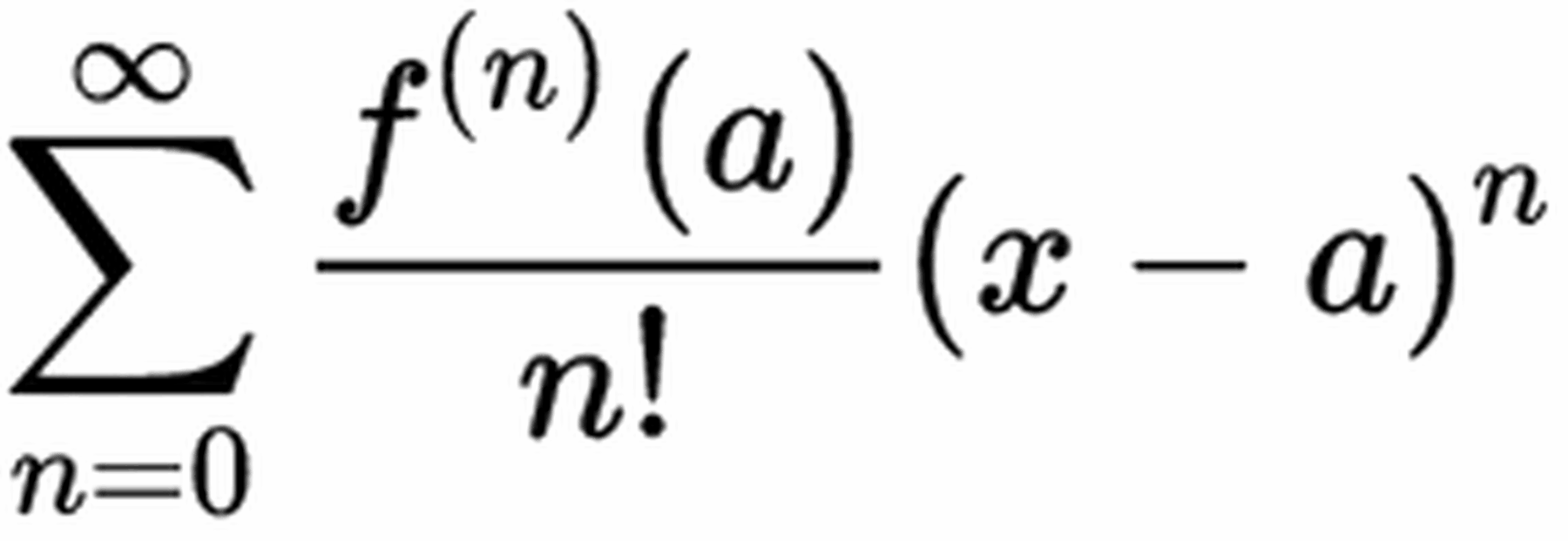Euler’s Formula by Abigail McKee

This is Euler’s formula: e^ix = cos x + i sin x (where x is a complex number)

It was thought up by the mathematician Leonhard Euler, and first published in 1748. This formula is useful because it links the exponential function f(x) = e^x and the trigonometric functions, allowing it to be used in maths and physics to simplify calculations, or to trace a unit circle.

Euler History

Leonhard Euler, born in 1707, was one of the greatest mathematicians of his time, due to his discovery of formulae such as this which are now used ubiquitously throughout maths and physics. Born in Switzerland, he began university at 13 with Johann Bernoulli, the younger brother of the man who discovered Euler’s number, e. In 1727, he moved to St Petersburg in Russia to take on a job in the Imperial Russian Academy, an institute intended to improve the quality of education in Russia, and which still runs to this day. During his time here, he solved the famous problem The Seven Bridges of Konigsberg, and began the study of graph theory, which is how I got to know about him through a Murderous Maths book. However, political troubles in Russia caused him to move to the Berlin Academy in Germany in 1741, where he published his famous formula above. After moving back to Russia in 1766, the political mess having calmed, he lived out the rest of his days with his wife (who died before him), his second wife and children. Despite having become almost completely blind at this point, he was still one of the first people to have used what we now know as Venn diagrams. His work even affected us students, him having promoted the use of pi to represent the ratio of a circle to its diameter, and having introduced f(x) function notation.

What are e and i?

Euler’s Formula involves two letters not taught at GCSE, e and i. These numbers are special in different ways. e is known as Euler’s number, as he was the first to use this letter to represent it. The number is irrational and begins 2.71828. It can be represented by (1 + 1/n)ⁿ. As n approaches infinity, so does this expression approach the value of e. However, despite being known as Euler’s number, e was introduced into the mathematical world half a century earlier, by Jacob Bernoulli, and this was because it had shown up in a different branch of mathematics- finance. In fact, e seems to appear everywhere, such as in the natural exponential function, probability theory, and working out radioactive half-lives. Bernoulli discovered it due to its similarity with a compound interest formula (1 + r/n)ⁿ, where r is the annual interest rate as a decimal, and n is the number of times interest is paid in a year. As you can see, if the interest rate was (a ridiculous) 100%, you would end up calculating a value close to e, the more often your interest was paid.

i is a different kettle of fish, in that it is an imaginary number that cannot be measured, because it is the square root of -1. The use of i to represent this number is also due to Euler, but imaginary numbers were known about since before Isaac Newton. It is also used in multiple fields, notably electrical engineering, where it is written as j because i is used to denote current. One important use of it that you will need to know about for Euler’s formula is complex numbers. As i is not real, to use it we can write all real numbers as complex numbers, which are written in the form a + bi. For example, 1 as a complex number would equal 1 + 0i. You can plot these on a complex plane, which is similar to a normal coordinates plain except the y axis goes up in multiples of i, so the a part represents the x-coordinate and the bi part represents the y-coordinate.

Deriving Euler’s Formula

To derive Euler’s Formula, we can use Taylor series to represent cos x and i sin x. A Taylor series is a representation of a function as an infinite sum of terms, given by the formula

For example, let’s take the cos function, and let x = 0: f(x) = cos x

(NOTE: THIS IS ALL IN RADIANS, and is more an approximation than an actual proof.)

Here is the value of the function and its first four derivatives:

f(0) = cos 0 = 1 f’(0) = -sin 0 = 0 f’’(0) = -cos 0 = -1 f’’’(0) = sin 0 = 0 f’’’’(0) = cos 0 = 1

This is because with radians differentiating sin x gives you cos x, and cos x gives you -sin x.

Substituting the first value into our list gives us 1/0! * (x-0)⁰, which equals 1*1 = 1.

The second value gives us 0/1! * (x-0)¹, which equals 0*1 = 0.

The third, fourth, and fifth values give us -x²/2!, 0, and x⁴/4! respectively.

If we add these first five terms together, we get f(x) = 1 – x²/2! + x⁴/4!. Sequences have patterns; we can guess the pattern the rest of the cos x sequence will follow: the powers and factorials will increase by 2 each time, and the signs will swap too. This gives us the cos sequence.

Using the same formula, the sin sequence = x – x³/3! + x⁵/5!… with powers and factorials increasing by 2 each time, and the signs swapping. However, Euler’s formula requires i sin x, so to find that, we multiply the sin sequence by i to give ix – ix³/3! + ix⁵/5!..., the i sin sequence. Adding these two sequences together gives 1 + ix - x²/2! – ix³/3! + x⁴/4! + ix⁵/5!..., but this doesn’t help us find e^ix. If you remember, i is equal to the square root of -1, so using the exponents of i we can substitute this into our big sequence to change all the terms to positive, like so:

f(x) = 1 + ix + (ix)²/2! + (ix)³/3! + (ix)⁴/4! + (ix)⁵/5!...

Because the exponents of i are as follows: i¹ = i, i² = -1, i³ = -1 * i = -i, i⁴ = 1, and i⁵ = i. Squaring and cubing i would make the second and third terms negative, so we can put the i’s in brackets.

Remember how to find the Taylor series? We are now going to find the series of e^ix. To start with, let’s find the e^x series: to do this we will need to know the derivative of the function e^x: this, conveniently, doesn’t change! f(x) to any derivative, when f(x) = e^x, will always be e^x. The derivative of e^ix, following the chain rule, is ie^ix.

Therefore, substituting e^x into the formula gives us 1 + x + x²/2! + x³/3! + x⁴/4! + x⁵/5!...

So, changing the power of e^x to e^ix should give us: 1 + ix + (ix)²/2! + (ix)³/3! + (ix)⁴/4! + (ix)⁵/5!... This is equal to the sum of the cos and i sin series, so e^ix = i sin x + cos x

Tracing a circle:

Now let’s look at something we can do with this formula. I mentioned a unit circle earlier, and now we will look at how it can be used to find roots of unity, which are the roots of expressions of the form xⁿ – 1.

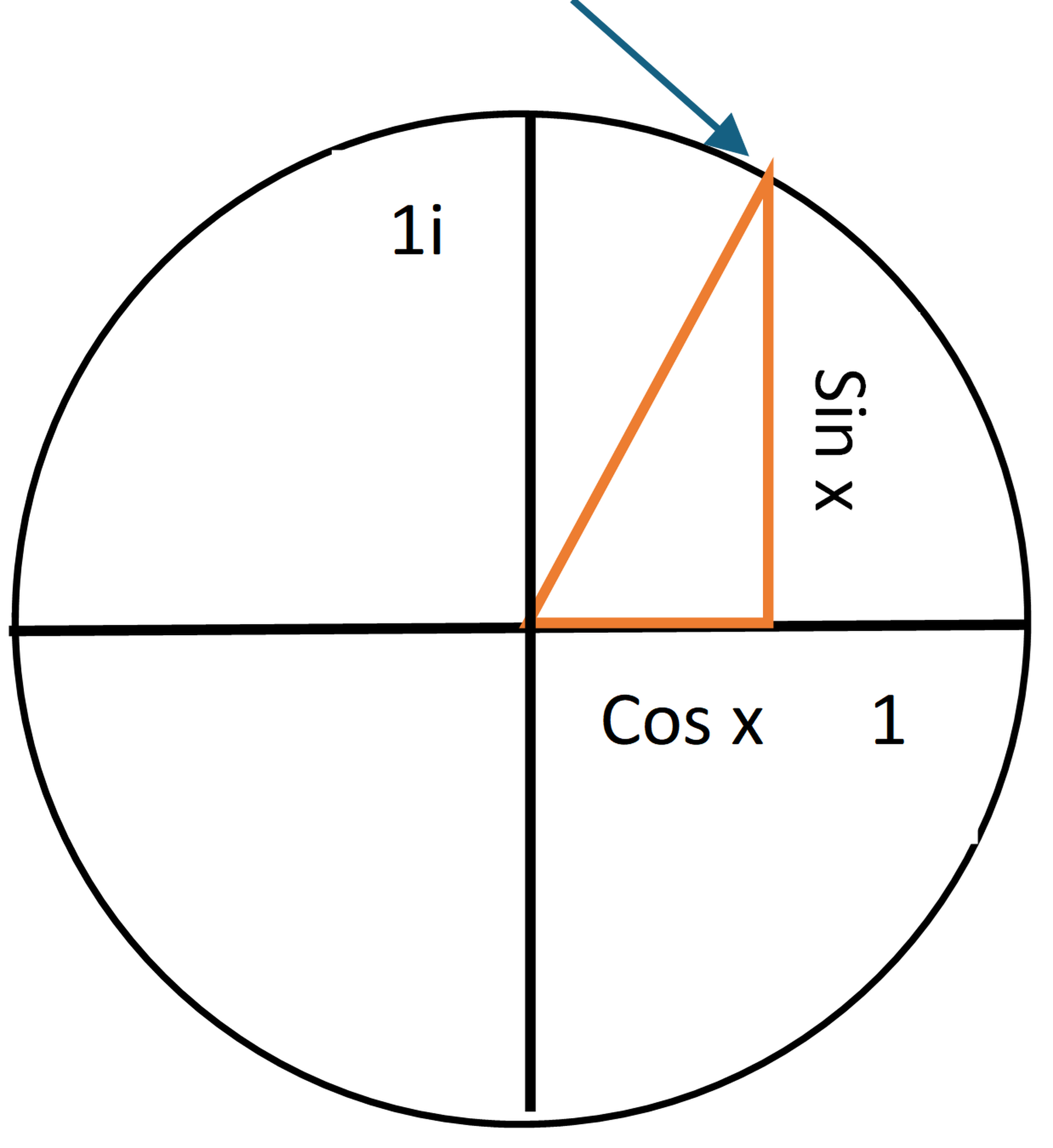
GCSE Further Maths tells us that an angle of any size can be defined by a point on a unit circle, forming a right-angled triangle with the radius, its position along the x axis, and its position along the y axis, where y = sin (theta) and x = cos (theta).

Using the complex plane discussed in the paragraph on imaginary numbers, we can represent complex numbers in the same way. Let your complex number x (remember, in the form a + bi) be represented by e^ix, which is of course the sum of cos x, which is a real number, and i sin x, which is an imaginary number. Let your x coordinate be cos x, and your y coordinate be i sin x, and that pair of coordinates is e^ix.

To relate this to roots of unity, we could take an example and look at the roots of x² – 1 = 0. x² = 1, so x must equal the square roots of 1, which are +1 and -1. Turning these into complex numbers gives us 1 + 0i and -1 + 0i, which can be plotted at the rightmost and leftmost points on our unit circle, dividing it into 2. We could also try x⁴ – 1 = 0, so x⁴ = 1, and if we square root this, x² = +1 or -1. This is where i comes in- the square roots of 1 are +1 and -1, but a square root of -1, as discussed, is i. -i is also a root of -1, as much like squaring real numbers the double negative cancels out, and still results in -1. So here we have four points, in complex numbers: 1 + 0i, 0 + 1i, -1 + 0i, and 0 - 1i. If we plot all of these, we see they form where the circle circumference crosses the axes, dividing it into four. This is the case for all roots of unity- they divide the circumference into equal parts, the number of which depends on the power of x. We can divide the circle into n equal angles in radians, work out the angles’ cos and sin, and find the point on the unit circle the angles match up to, which will be roots of unity of the equation xⁿ – 1 = 0.

I chose to write about Euler’s formula after coming across it unintentionally, at first looking at the Bridges of Konigsberg problem. However, this formula seemed interesting to me because it involved e and i, which I had not come across before, graphs, which helped me to visualise what I was learning about, and gave me a real example of using radians. Looking into Euler’s formula has been fun, interesting, and more than a little challenging, and I had a great time writing this.